Rumus volume tabung – Hai hai kami kembali lagi nih untuk menyajikan informasi-informasi menarik untuk pembaca sekalian. Tapi pada kesempatan yang berbahagia ini kami masih akan membahas tentang rumus.
Setelah sebelum-sebelumnya kami juga membahas berbagai rumus matematika, rumus dalam excel, sampai juga rumus slovin. Dan rumus yang akan kami paparkan kali ini merupakan rumus yang sering kita jumpai di pelajaran matematika.
Siapa sih yang gak tahu tentang tabung. Ya tabung merupakan salah satu bangun ruang yang sudah kita pelajari sejak sekolah dasar.
Di bangku sekolah dasar kita mulai mengenali bagaimana bentuk tabung. Lalu semakin tinggi kelas, kita juga akan belajar bagaimana cara menghitung volume tabung tersebut dengan sebuah rumus-rumus.
Bahkan di sekolah tingkat lanjutan pun tabung ini masih terus dipelajari meskipun dengan kerumitan yang berbeda. Tetapi rumus dasarnya tentu sudah dipelajari sejak SD.
Meskipun begitu, kita tentu bisa saja lupa mengenai rumus tabung ini dan bagaimana cara menghitungnya. Oleh karena itu kami ingin mengingatkan teman-teman yang barangkali lupa atau memang belum memahami rumus volume tabung.
Kami akan mencoba menguraikan rumus-rumus dalam menghitung sebuah tabung dari yang paling sederhana atau dasar sampai juga rumus tabung yang sedikit rumit.
Siap ya untuk belajar mengenai tabung dengan riang gembira. Kalau begitu yuk simak terus tulisan di bawah ini sampai habis ya.
Apa Itu Bangun Ruang Tabung?
Hal sederhana yang harus diketahui tentang suatu hal adalah pengertian atau definisi dari sesuatu tersebut. Dan karena itu kami terlebih dahulu akan memberikan pengertian tentang apa itu bangun ruang yang berbentuk tabung.
Jadi tabung merupakan bangun ruang yang memiliki dua bidang pembatas berbentuk lingkaran, yang satu sebagai sisi alas, lalu lainnya sebagai sisi atas, dan juga memiliki bidang lengkung sebagai sisi tegak yang disebut dengan selimut tabung.
Bagaimana Gambar Tabung?
Supaya deskripsi di atas bisa tergambarkan dengan jelas, kami juga sudah menyiapkan gambar tabung seperti di bawah ini:
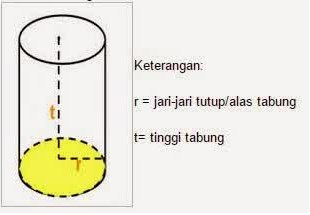
Dari gambar di atas kita bisa mencermati kemudian membayangkan jika kedua bidang atas dan alas dipotong, dan selimut tabung tersebut dibuka dan diletakkan pada bidang datar maka akan terlihat jaring-jaring tabung. Berikut terdapat gambar yang bisa mudah dipahami:
Bidang sisi atas dan alas berbentuk lingkaran dan memiliki jari-jari yang sama. sedangkan tinggi tabung ini merupakan jarak antara titik pusat lingkaran atas dan alas.
Semoga dengan penggambaran secara detail mengenai bentuk tabung ini nantinya bisa memudahkan teman teman dalam memahami rumus-rum yang digunakan untuk menghitung volume, luas, tinggi, atau jari-jari tabung. Untuk memahami lebih dalam lagi mengenai tabung ini tetap simak artikel ini sampai habis yaa hehe.
Sifat Sifat Tabung
Nah melihat penjelasan sebelumnya barangkali kalian juga sedikit banyak sudah memahami tentang sifat-sifat apa saja yang dimiliki oleh tabung ya. Meskipun begitu kami akan tetap mendeskripsikan sifat tabung tersebut dengan jelas. Jadi apa saja sih sifat sifat tabung?
- Pertama, tabung memiliki dua rusuk lengkung
- Kedua, tabung punya dua sisi berbentuk lingkaran dan satu sisi berbentuk bidang lengkung
- Dan terakhir, tabung tidak memiliki titik sudut.
Untuk lebih memudahkan teman teman dalam memahami penjelasan di atas kami akan menyertakan gambar yang memuat bagian-bagian dari tabung secara rinci, kami berharap gambar tersebut bisa membantu.
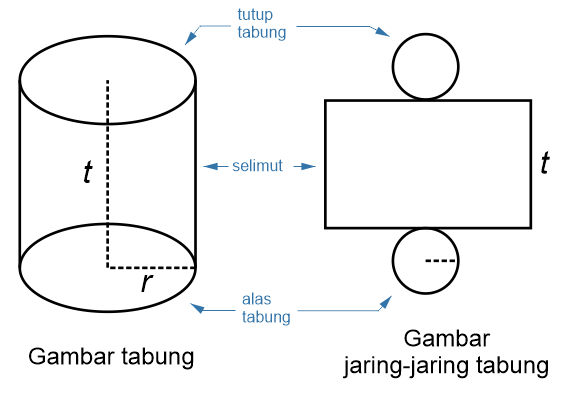
Cara Membuat Tabung yang Sederhana
Tips atau langkah membuat tabung sederhana ini sangat cocok untuk teman-teman yang mengajar matematika untuk adik-adik di bangku sekolah dasar.
Karena pembelajaran dengan praktik merupakan metode pembelajaran yang cukup efektif. Atau teman-teman pengajar juga bisa memberikan contoh produk atau barang yang berbentuk tabung seperti kaleng sarden, botol, dan lain sebagainya.
Tetapi tak ada salahnya juga kalau sekalian membuat tabung sendiri dengan bahan yang sederhana. Adapun langkah-langkah dalam membuat tabung adalah sebagai berikut:
- Pertama, yuk siapkan beberapa bangun datar. Lalu bentuk dua bidang menjadi lingkaran keduanya memiliki sisi sama. Lalu bentuk juga satu persegi panjang yang kelilingnya sama dengan lingkaran.
- Kemudian, sisi lebar yang ada pada persegi panjang sambungkan dengan menggunakan lem. Kalau sudah tersambung dan membentuk selimut, pasangkan kedua lingkaran pada bagian atas dan bawah.
- Dan taraaaa sudah selesai deh, hasilnya bisa dilihat pada gambar berikut:
Rumus Luas Permukaan Tabung
Sebelum kita belajar tentang rumus volume tabung, alangkah baiknya kalau kita harus mengetahui terlebih dahulu rumus luas permukaan tabung. Karena rumus luas tabung ini yang nantinya menjadi dasar bagi rumus volume tabung.
Adapun rumus luas permukaan tabung adalah sebagai berikut:
L=2πr (r+t)
Adapun keterangan dari lambang di atas adalah:
π = 22/7 atau 3,14
r = radius atau jari-jari lingkaran
t = tinggi tabung
untuk mendapatkan nilai jari-jari, kamu bisa mencarinya dengan rumus berikut:
r = d (diameter) : 2
sedangkan untuk mencari diameter kebalikannya yaitu 2xr.
Rumus Volume Tabung
Tiba saatnya untuk mengetahui dan mempelajari seperti apa formula atau rumus dalam menghitung volume tabung. Sebenarnya rumus ini sangat mudah kok, jadi tak perlu cemas dan khawatir dalam mempelajari rumus ini. berikut adalah formula rumus volume tabung:
Volume tabung = volume prisma, jadi
Volume tabung = luas alas x tinggi
= πr2 x t
Contoh Soal Volume Tabung
Sebuah tabung memiliki jari jari alas 49 cm, dan memiliki tinggi 200 cm. Jika tabung tersebut diisi dengan air maka berapa liter air yang dapat ditampung dalam tabung tersebut?
Jawab:
Diketahui:
r = 49 cm
t = 200 cm
V = πr2 x t
V = 22/7 x 492 x 200
V = 1.509.200 cm3 = 1.509,2 dm3
V = 1.509,2 liter
Macam-Macam Rumus Tabung
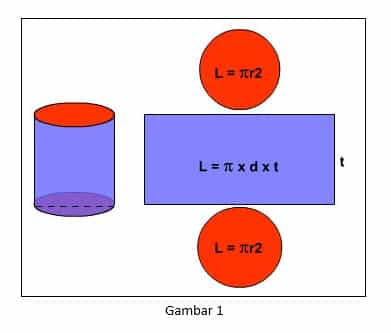
Selain rumus luas permukaan tabung dan volume tabung masih banyak sekali bagian dari tabung yang bisa kita cari hitungannya berdasarkan rumus. Seperti yang telah dijelaskan di atas kita bisa mencari luas selimut tabung, panjang jari-jari tabung, dan lain sebagainya.
Berikut kami rangkum beberapa rumus yang bisa digunakan ketika terdapat beberapa pertanyaan yang sering muncul dalam soal-soal bangun ruang tabung, sekaligus disertai dengan contoh soalnya:
- Mencari Luas Selimut tabung
Ls = π x d x t
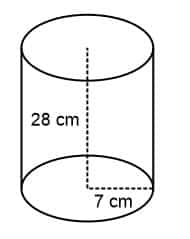
Contoh soal:
Diketahui sebuah tabung dengan jari-jari 7 cm dan tinggi 28 cm, berapakah luas selimut tabung tersebut.
Jawab:
Ls = π x d x t
= 22/7 x 7/2 x 28
= 22/7 x 3,5 x 28
= 308 cm
- Mencari Luas Alas
La = π x r x r
- Mencari Luas Tanpa Tutup
L.tanpa tutup = La + Ls
- Mencari jari- jari yang diketahui volumenya
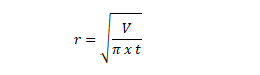
- Jari-jari yang diketahui luas selimutnya
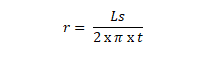
- Mencari tinggi yang diketahui volumenya
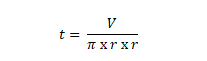
- Tinggi diketahui luas selimutnya
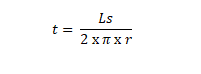
- Tinggi diketahui luas permukaannya
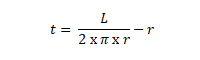
Penutup
Bagaimana penjelasan mengenai rumus volume tabung di atas? kami pikir rumus tabung yanng kami sajikan cukup komplit dan beragam.
Karena itu harapannya teman-teman setelah ini tidak hanya bisa menghitung volume tabung, tetapi juga menghitung luas permukaan, menghitung jai-jari tabung, dan lain sebagainya.
Atau paling tidak teman teman jadi tahu seperti apa bentuk tabung itu dan bagaimana rumus dasar untuk menghitung volumenya.
Dan demikianlah artikel yang bisa kami sajikan. Kami memohon maaf jika terdapat kesalahan. Sekali lagi semoga bermanfaat dan terimakasih telah membaca.
Originally posted 2020-07-01 14:31:36.
