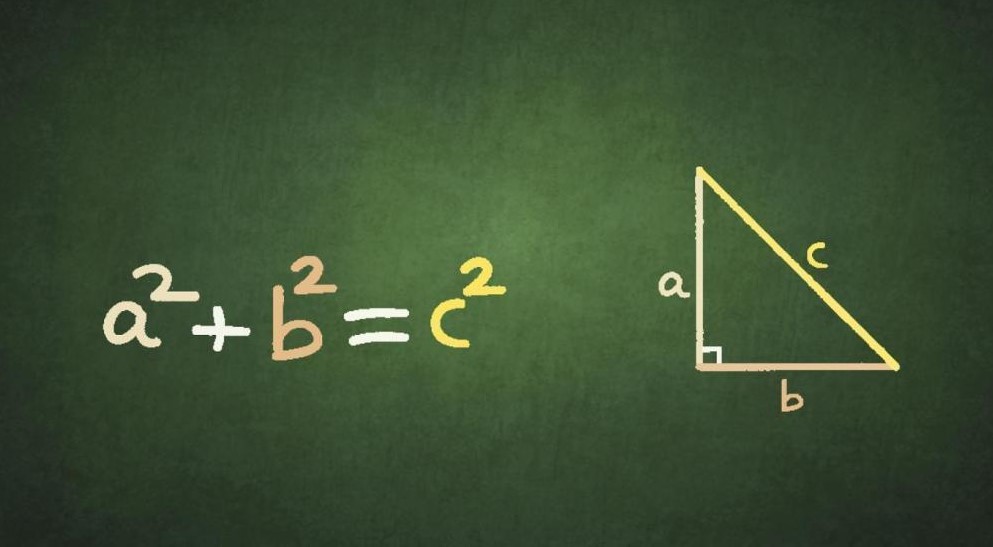Rumus Phytagoras – Halo teman-teman….senang sekali bisa berjumpa dengan anda kembali. Perjumpaan kali ini masih seputar hitung-hitungan ya, yakni rumus Phytagoras.
Rumus Phytagoras atau yang sering disebut juga dengan dalil teorema Pythagoras sepertinya tidak asing lagi bagi kita.
Tentunya materi Phytagoras sudah dipelajari sejak duduk dibangku Sekolah Dasar (SD) dan merupakan materi pelajaran matematika yang diajarkan paling awal.
Bisa dikatakan Phytagoras ini tidak rumit dan cukup mudah untuk dipahami. Rumus Phytagoras sering dipergunakan dalam materi hitungan geometri.
Dimana terdapat persoalan yang meminta untuk melakukan perhitungan keliling dari bangun datar segitiga siku-siku yang panjang sisi miringya belum diketahui.
Tak hanya sering digunakan ketika materi perhitungan geometri tetapi bahasan Phytagoras juga terdapat pada materi trigonometri yang dipelajari ketika duduk di bangku SMA.
Mungkin banyak dari kita yang lupa akan materi tentang Phytagoras ini. Hal ini mungkin disebabkan karena sangat jarang atau bahkan hampir tidak ada persoalan yang secara langsung menanyakan untuk menghitung atau menentukan panjang sisi miring sebuah siku-siku.
Nah, jika anda melupakan materi bahasan rumus Phytagoras atau bahkan belum paham tentang materi tersebut, anda perlu menyimak penjelasannya berikut ini.
Sebelum kita membahas atau mengulas kembali rumus Phytagoras, mari kita simak sejarah singkat munculnya rumus Phytagoras ini.
Sejarah Phytagoras

Nama Phytagoras mungkin sudah pernah didengar kebanyakan orang. Phytagoras adalah sebuah nama orang yang berasal dari zaman yunani kuno sekitar tahun 570 – 495 sebelum masehi (SM).
Phytagoras ini bukan orang biasa, ia merupakan tokoh filsuf dan juga seorang ilmuwan matematika yang sangat cemerlang pada masanya.
Ia adalah penemu rumus Phytagoras. Hal tersebut dibuktikan dengan penemuannya yang telah berhasil memecahkan permasalahan panjang sisi segitiga siku-siku dengan formula yang bisa dikatakan sangat sederhana.
Dalil Phytagoras
Dalil Phytagoras atau yang sering disebut juga dengan teorema Phytagoras adalah sebuah teorema atau dalil
Matematika yang menunjukkan adanya hubungan yang terjadi antar sisi pada sebuah segitiga siku-siku.
Menurut dalil atau teorema Phytagoras , kuadrat sisi miring pada sebuah bangun dtara segitiga siku-siku adalah jumlah kuadrat pada kedua sisi lainnya.
Atau dengan kata lain panjang alas kuadrat tambah panjang tinggi kuadrat pada segitiga siku-siku sama dengan panjang sisi miring kuadrat.
Coba perhatikan penjelasnnya berikut ini. Misalkan , panjang tinggi segitiga adalah a (vertikal), panjang alasnya adalah b (horizontal) dan panjang sisi miringnya adalah c.
Maka dengan menggunakan dalil atau teorema pytaghoras, hubungan antara ketiga sisinya dapat dirumuskan menjadi a2 + b2 = c2.
Berdasarkan rumus tersebut terbukti bahwa sisi miring sebuah segitiga siku – siku ialah akar dari jumlah kuadrat sisi – sisi yang lain. Untuk lebih jelasnya perhatikan gambar di bawah ini :

nah, setelah membahas sejarah singkat rumus Phytagoras dan juga dalil atau teorema Phytagoras, selanjutnya kita akan membahas lebih lanjut terkait rumus dan cara menggunakan rumus Phytagoras.
Rumus Phytagoras

Pada dasarnya Rumus Phytagoras a2 + b2 = c2, dapat dinyatakan dalam beberapa bentuk, yaitu:
- a2 + b2 = c2
- c2 = a2 + b2
- a2 = c2 – b2
- b2 = c2 – a2
Untuk menyelesaikan masing-masing dari rumus di atas, dapat digunakan nilai akar dari rumus Phytagoras tersebut. Rumus Pythagoras dalam bentuk akar, jika :
- Sisi tegak dan mendatarnya ialah a dan b
- Sedangkan sSisi miringnya adalah c
Maka rumus yang dihasilkan adalah sebagai berikut:


Perlu dicatat dan diingat ya teman-teman bahwa rumus Phytagoras hanya bisa berlaku pada bangun datar segitiga siku-siku.
Triple Phytagoras (Pola Angka)
Dalam dalil atau teorema pythagoras, ada pola angka atau yang dikenal juga dengan Triple Phytagoras (Pola angka).
Tripel Phytagoras adalah sebutan untuk pola angka a-b-c yang memenuhi rumus pythagoras di atas.
Tripel Phytagoras perlu untuk teman-teman ingat agar dalam memecahkan soal pythagoras akan lebih gampang dan cepat dalam mengerjakannya.
Ada banyak sekali angka yang memenuhi tripel pytaghoras ini. Beberapa contohnya dapat anda lihat tabel di bawah ini.
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 6 | 8 | 10 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
| 9 | 12 | 15 |
| 10 | 24 | 26 |
| 12 | 16 | 20 |
| 14 | 48 | 50 |
| 15 | 20 | 25 |
| 15 | 36 | 39 |
| 16 | 30 | 34 |
| 17 | 144 | 145 |
| 19 | 180 | 181 |
| 20 | 21 | 29 |
Daftar pola angka diatas tentunya masih banyak dan masih bisa dilanjutkan sampai angka yang sangat besar.
Jika anda belum paham atau belum mengerti masksud dari angka-angka tersebut, anda bisa mencoba untuk memasukkan angka-angka atau nilai tersebut pada rumus a2 + b2 = c2.
Sederhananya angka-angka tersebut akan sesuai ketika anda memasukkan nilainya pada rumus Phytagoras.
Contoh Soal Rumus Phytagoras
Setelah anda mengetahui bagaimana sejarah singkat, dalil atau teorema serta rumus Phytagoras, anda juga perlu menyimak beberapa contoh soal rumus Phytagoras beserta jawabanya dibawah ini.
Agar anda lebih memahami penggunaan rumus Phytagoras ini.
Contoh 1
Sebuah bangun datar segitiga mempunyai panjang sisi AC 12 cm dan sisi BC panjangnya 5 cm. Hitunglah sisi miring dari segitiga tersebut (AB) ?
Jawaban :
Diketahui : AC = 12 cm dan BC = 5 cm, diitanya : Panjang sisi miring AB ?
Cara pertama :
AB2 = BC2 + AC2
= 52 + 122
= 25 + 144
= 169
AB =√169
= 13
Cara kedua
AB =√ BC² + AC²
AB =√ 52 + 122
AB =√ 25 + 144
AB =√ 169
AB =13
Jadi, panjang sisi AB (miring) pada segitaga tersebut adalah 13 cm.
Contoh 2
Berapakah panjang sisi tegak sebuah segitiga siku – siku, jika diketahui sisi datarnya adalah 9 cm dan panjang sisi miringnya 15 cm?
Jawab:
Misalnya : c = sisi miring, b = sisi datar, a = sisi tegak
Diketahui : c = 15 cm dan b = 9 cm, ditanya : a = ?
Cara Pertama :
a² = c² – b²
a² = 225 – 81
a² = 144
a = √ 144
a = 12
Cara Kedua :
a =√ c² – b²
a =√ 225 – 81
a =√ 144
a =12
Sehingga, panjang sisi tegak segitiga tersebut adalah 12 cm
Contoh 3
Diketahui terdapat tiga buah kota (A, B, C) yang membentuk segitiga, dengan siku di kota B. Jarak kota AB = 16 km, sedangkan jarak kota BC adalah 12 km. Berapakah jarak kota AC?
Jawab :
Anda bisa menggunakan rumus teorema pytagoras
Diketahui : AB = 16 km dan BC = 12 km, ditanya : AC?
AC =√ BC² + AB²
AC =√ 162 + 122
AC =√ 256 + 144
AC =√ 400
AC =20
Jadi, dapat diketahui bahwa jarak kota AC = 20 km.
Bagaimana teman-teman? Apakah anda sudah paham dengan rumus Phytagoras, cukup mudah bukan? Saya harap anda benar-benar sudah paham dan mengerti materi di atas ya.
Anda juga bisa lebih banyak lagi untuk mencari dan memecahkan persoalan-persoalan bahasan phyagoras dari berbagai sumber.
Demikian perjumpaan kita kali ini tentang rumus Phytagoras beserta contoh soalnya. Sampai jumpa pada kesempatan lain yang menggembirakan.