Diagram venn – mungkin banyak dari kita yang sudah pernah mendengar istilah tersebut, meskipun tidak semuanya bisa membuatnya atau lupa bagaimana caranya.
Materi ini bisa dijumpai pada tingkat sekolah menengah pertama, tepatnya kelas tujuh. Dulu diagram venn merupakan salah satu materi favorit mimin.
Kenapa? Karena mudah dipahami hehe. Bagaimana menurut teman-teman? Apakah juga demikian? Walaupun kalian menganggap sebaliknya, tak perlu khawatir.
Karena pada kesempatan yang berbahagia ini kami kembali lagi untuk membahas tentang materi diagram venn.
Dalam ilmu matematika materi ini penting untuk dipelajari, ia bisa menggambarkan suatu hubungan logika.
Jadi kami pikir diagram venn penting untuk dipelajari, karena nantinya bisa melatih kerangka berpikir kita dalam segala hal.
Termasuk juga dalam kehidupan sehari-hari. Tetapi memang diagram venn ini biasanya lebih sering digunakan dalam bidang matematika, aplikasi komputer, dan statistika, misalnya untuk penyajian data statstik.
Untuk mengetahui lebih jelas lagi apa yang dimaksud dengan diagram venn, dan bagaimana cara membuatnya, simak uraian di bawah ini
Apa Itu Diagram Venn?

Mulanya diagram venn ini pertama kali diperkenalkan oleh matematikawan asal ingris bernama John Venn. Jadi nama diagram ini diambil dari nama yang memperkenalkannya ke publik.
Lalu apa sih sebenarnya diagram venn itu? seperti yang diketahui bahwa diagram venn adalah sebuah gambar yang menunjukkan ekspresi hubungan antar himpunan dalam objek yang punya nilai atau jumlah yang sama.
Sebagaimana yang sudah disinggung sebelumnya biasanya diagram ini digunakan untuk menyajikan data ilmiah secara statistik.
Himpunan
Dalam mempelajari diagram venn teman-teman akan menemukan istilah himpunan. Himpunan merupakan hal yang akan menjadi unsur penting dalam diagram ini.
Lalu apa yang dimaksud dengan himpunan? Apakah dia suatu kelompok? ya secara maknanya anggota dari himpunan memang lebih dari satu.
Namun secara definitif himpunan merupakan sekumpulan objek yang bisa diartikan dengan jelas. contohnya alat elektronik yang kipakai sehari-hari bisa menjadi himpunan, karena di dalamnya terdapat televisi, kulkas, handphone, laptop, dan lain sebagainya.
Himpunan tersebut jika ditulis secara matematis menjadi {televisi,kulkas,handphone,laptop…}
Contoh lain himpunan dalam matematika dengan menggunakan bilangan misalnya:
Himpunan bilangan prima = {2,3,5,7,9,11,13,17….}
Himpunan semua bilangan = {1,2,3,4,5,6,7,….}
Cukup mudah kan ya untuk memahami apa itu himpunan, nah himpunan di atas kemudian bisa digambarkan dalam diagram venn supaya lebih mudah dan praktis untuk dibaca.
Bentuk Diagram Venn
Selanjutnya kita akan mempelajari berbagai macam bentuk dari diagram venn. Diagram ini memang memiliki bentuk yang sangat beragam berdasarkan dari jenis himpunannya.
Jadi memang bentuk diagram ini bisa dilihat dari jenis himpunannya. Adapun apa saja bentuk diagram tersebut? yuk perhatikan di bawah ini:
Himpunan bagian
Bentuk diagram yang pertama akan kami jelaskan adalah bentuk himpunan bagian. Konsep atau syarat dalam himpunan bagian adalah:
“himpunan A bisa disebut bagian dari himpunan B, jika semua anggota A adalah anggota dari himpunan B”
Contohnya:
A = {1,2,3,4,5,}
B = {1,2,3,4,5,6,7,8,9,10}
Adapun gambar diagram venn yang merupakan himpunan bagian dapat dilihat di bawah ini:

Himpunan yang sama
Kemudian selanjutnya adalah bentuk diagram venn yang memiliki himpunan yang sama. Diagram ini bisa dibaca dengan pernyataan apabila himpunan A dan B terdiri dari anggota yang sama. Sehingga dengan kata lain anggota B adalah anggota himpunan A.
Contohnya:
A = {4,5,6}
B = {5,6,4}
Jika kondisi himpunan demikian, secara matematis dapat ditulis A=B. Adapun bentuk diagram venn himpunan sama adalah sebagai berikut:

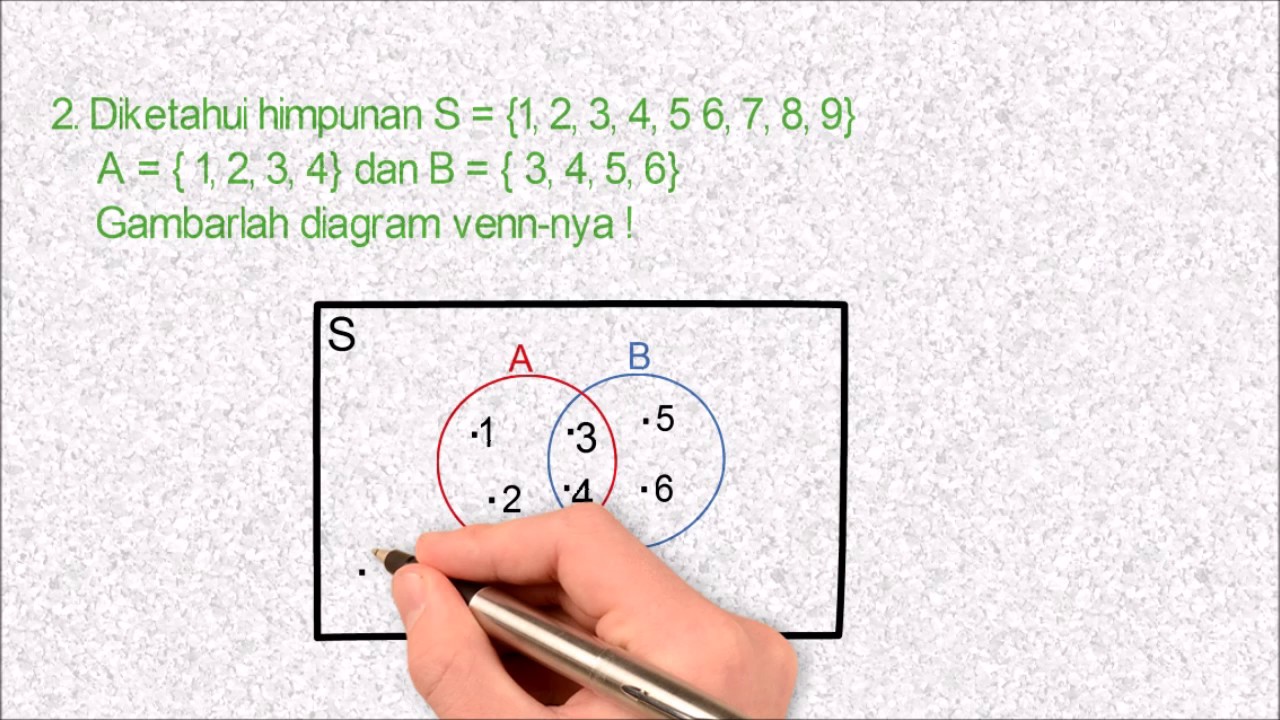
Himpunan saling berpotongan
Gambar dari diagram venn ini memang saling berpotongan. Mengapa demikian? Karena di antara dua himpunan terdapat suatu kesamaan. Himpunan anggota yang memiliki kesamaan dengan anggota B berarti termasuk dalam himpunan B.
Contohnya begini:
A = {1,2,3,4,5,6,7,8,9}
B = {3,6,9,12,15,18,21}
Hal ini berarti anggota A yakni {3,6,9} masuk ke dalam himpunan B. Adapun diagram yang himpunannya saling berpotongan adalah sebagai berikut:

Himpunan saling lepas
Seperti apa itu himpunan saling lepas? Jadi diagram yang himpunannya saling lepas berarti anggota himpunan A tidak memiliki kesamaan sama sekali dengan anggota himpunan B.
Contohnya:
A = {1,2,3,4,5,6,7}
B = {8,9,10,11,12,13,14,}
Jika kondisi demikian maka secara matematis dapat ditulis dengan A//B. Adapun gambar dari diagram ini dapat dilihat di bawah ini:

Bentuk Diagram Venn: Himpunan yang ekuivalen
Eits jangan kemana-mana dulu ya karena masih ada bentuk diagram yang lain loh ya, kali ini bentuk diagram dengan himpunan yang ekuivalen.
Suatu himpunan bisa dikatakan demikian jika jumlah anggota himpunan A sama dengan jumlah anggota B. Himpunan jenis ini akan ditulis secara matematis seperti ini n(A) = n(B)
Adapun di bawah ini terdapat juga hubungan antar himpunan:
Gabungan
Apa itu yang dimaksud dengan gabungan himpunan? Merupakan himpunan yang anggota-anggotanya adalah termasuk dalam himpunan A atau himpunan B atau bahkan keduanya.
Misalnya himpunan A = {1,2,3,4,5,6,7}, dan himpunan B = {2,3,4,5,6,7,8}. Nah jika kondisi demikian maka himpunan A dan B digabungkan, sehingga membentu himpunan baru yaitu A∪B={1,2,3,4,5,6,7,8}.
Dan notasi dari gabungan himpunan A dan B adalah A∪B= {x│x ∈A atau x ∈B}. Berikut ini juga kami lampirkan contoh gambar diagram yang merupakan gabungan himpunan:

Irisan

Hubungan himpunan yang akan dipelajari selanjutnya disebut dengan irisan. Irisan himpunan merupakan himpunan yang anggotanya masuk dalam himpunan A dan himpunan B.
Simbol dari irisan himpunan A dan himpunan B dapat ditulis dengan simbol A ∩B. Untuk lebih memahami apa yan dimaksud dengan irisan himpunan perhatikan contoh berikut:
A = {2,3,5,7,11,13,17}
B = {1,2,3,4,5}
Berdasarkan dua himpunan di atas dapat diketahui bahwa anggota A yang sama dengan anggota himpunan B adalah 2, 3, 5. Karenanya dapat ditulis bahwa A ∩B = {2,3,5}
Komplemen

Dan terakhir adalah hubungan himpunan dengan jenis komplemen. Komplemen himpunan A atau ditulis dengan Ac adalah suatu himpunan yang anggotanya adalah anggota himpunan semesta tetapi tidak masuk dalam anggota himpunan A.
Contohnya:
S (semesta) = {1,2,3,4,5,6,7,8,9,10}
A = {1,2,3,4,5}
Berdasarkan himpunan di atas kita bisa tahu bahwa terdapat anggota himpunan semesta dan himpunan A yang sama.
Karenanya anggota lainnya yang tidak sama tersebut membentuk himpunan baru yang disebut komplemen. Berarti komplemen dari himpunan A adalah {6,7,8,9,10}.
Bagaimana Cara Membuat Diagram Venn?
Sekarang pembahasan terakhir adalah bagaimana cara menggambar diagram tersebut? Sebenarnya mudah saja jika teman-teman sudah memahami bentuk dari diagram yang sudah dijelaskan di atas, dan juga bagaimana hubungan himpunannya.
Tetapi dasarnya untuk bisa menggambar diagram venn caranya adalah sebagai berikut:
- Gambarkan himpunan semesta dalam diagram venn dengan bentuk persegi panjang
- Lalu gambarkan setiap himpunan yang sedang dijelaskan dalam bentuk lingkaran atau kurva tertutup
- Dan terakhir anggota dari setiap himpunan diberikan tanda titik.
Penutup
Semoga pembaca sekalian dapat memahami materi yang telah disampaikan di atas. Tetapi kalaupun belum kami memohon maaf karena belum berhasil memberikan uraian dengan mudah.
Dan tentunya mari kita sama-sama belajar dengan lebih baik lagi. Demikianlah artikle tentang diagram venn yang bisa kami sajikan.
Semoga bisa bermanfaat untuk teman-teman semua, meskipun dalam tingkat yang sangat kecil. Selamat dan semangat belajar, jangan lupa berbahagia yaa.